Los puntos de Lagrange son posiciones en el espacio donde las fuerzas gravitacionales de un sistema de dos cuerpos como el Sol y la Tierra producen regiones mejoradas de atracción y repulsión. Estos pueden ser utilizados por naves espaciales para reducir el consumo de combustible necesario para permanecer en posición.
Los puntos de Lagrange se nombran en honor al matemático italo-francés Josephy-Louis Lagrange.
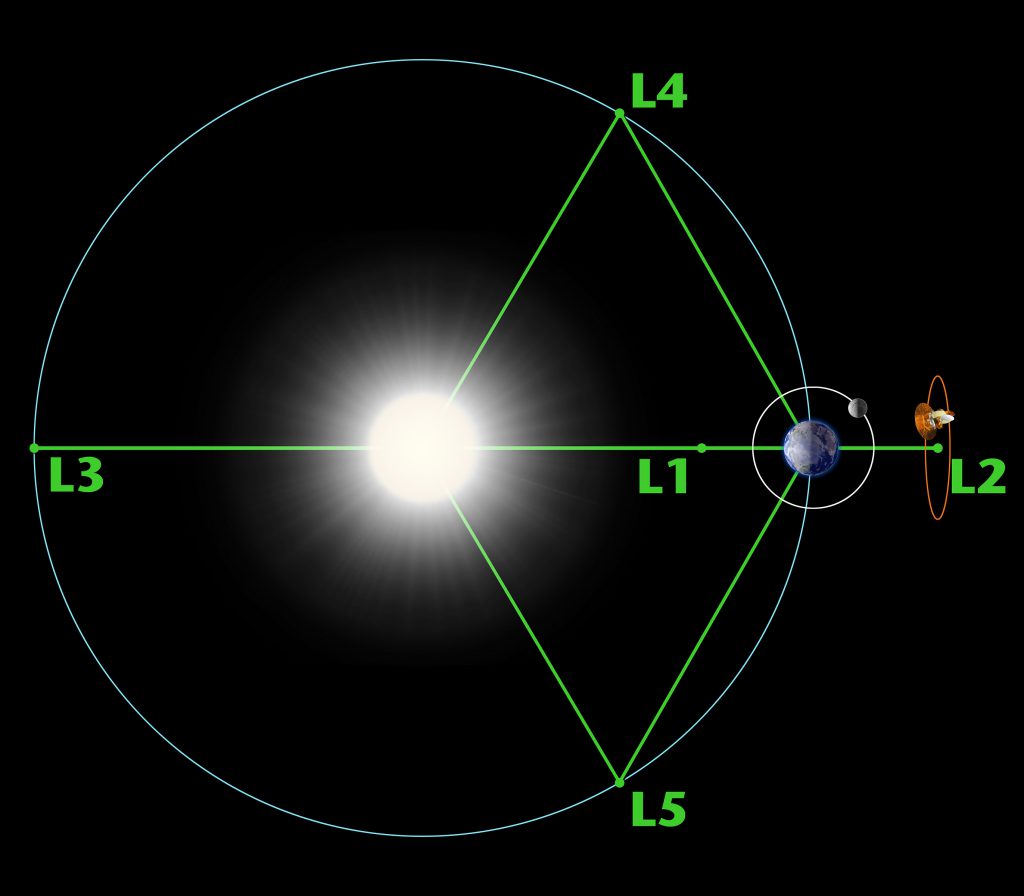
Hay cinco puntos especiales donde una pequeña masa puede orbitar en un patrón constante con dos masas más grandes. Los puntos de Lagrange son posiciones donde la atracción gravitacional de dos masas grandes es exactamente igual a la fuerza centrípeta requerida para que un objeto pequeño se mueva con ellas. Este problema matemático, conocido como el “Problema general de los tres cuerpos”, fue considerado por Lagrange en su artículo premiado (Essai sur le Problème des Trois Corps, 1772).
De los cinco puntos de Lagrange, tres son inestables y dos son estables. Los puntos inestables de Lagrange, etiquetados como L1, L2 y L3, se encuentran a lo largo de la línea que conecta las dos grandes masas. Los puntos estables de Lagrange, etiquetados como L4 y L5, forman el vértice de dos triángulos equiláteros que tienen las grandes masas en sus vértices. L4 lidera la órbita de la Tierra y L5 le sigue.
El punto L1 del sistema Tierra-Sol ofrece una vista ininterrumpida del sol y actualmente alberga el satélite SOHO del Observatorio Solar y Heliosférico.
El punto L2 del sistema Tierra-Sol fue el hogar de la nave espacial WMAP, actual hogar de Planck y futuro hogar del telescopio espacial James Webb. L2 es ideal para la astronomía porque una nave espacial está lo suficientemente cerca para comunicarse fácilmente con la Tierra, puede mantener al Sol, la Tierra y la Luna detrás de la nave espacial para obtener energía solar y (con el blindaje apropiado) proporciona una vista clara del espacio profundo para nuestros telescopios. Los puntos L1 y L2 son inestables en una escala de tiempo de aproximadamente 23 días, lo que requiere que los satélites que orbitan estas posiciones se sometan a correcciones regulares de rumbo y actitud.
Es poco probable que la NASA encuentre algún uso para el punto L3 ya que permanece oculto detrás del Sol en todo momento. La idea de un planeta oculto ha sido un tema popular en la escritura de ciencia ficción.
Los puntos L4 y L5 albergan órbitas estables siempre que la relación de masa entre las dos grandes masas supere 24,96. Esta condición se satisface tanto para los sistemas Tierra-Sol como Tierra-Luna, y para muchos otros pares de cuerpos del sistema solar. Los objetos que orbitan en los puntos L4 y L5 a menudo se denominan troyanos en honor a los tres grandes asteroides Agamenón, Aquiles y Héctor que orbitan en los puntos L4 y L5 del sistema Júpiter-Sol. (Según Homero, Héctor fue el campeón troyano asesinado por Aquiles durante el asedio de Troya por el rey Agamenón). Hay cientos de asteroides troyanos en el sistema solar. La mayoría orbitan con Júpiter, pero otros orbitan con Marte. Además, varias de las lunas de Saturno tienen compañeros troyanos.
En 1956, el astrónomo polaco Kordylewski descubrió grandes concentraciones de polvo en los puntos troyanos del sistema Tierra-Luna. El instrumento DIRBE en el satélite COBE confirmó observaciones anteriores de IRAS de un anillo de polvo que seguía la órbita de la Tierra alrededor del Sol. La existencia de este anillo está estrechamente relacionada con los puntos de Troya, pero la historia se complica por los efectos de la presión de la radiación sobre los granos de polvo.
En 2010, el telescopio WISE de la NASA finalmente confirmó el primer asteroide troyano (2010 TK7) alrededor del principal punto Lagrange de la Tierra.
Encontrar los puntos de Lagrange
La forma más fácil de entender los puntos de Lagrange es pensar en ellos de la misma manera que se pueden inferir las velocidades del viento a partir de un mapa meteorológico. Las fuerzas son más fuertes cuando los contornos del potencial efectivo están más cerca y más débiles cuando los contornos están muy separados.
Traducción no oficial con fines divulgativos del artículo original en Inglés.
Créditos: NASA / Neil J. Cornish – Wikinson Microwave Anistropy Probe team.